| Panagiotis Stefanides |

“GOLDEN ROOT SYMMETRIES OF GEOMETRIC FORMS”
By:
Eur Ing Panagiotis Ch. Stefanides BSc(Eng)Lon(Hons) CEng MIET
MSc(Eng)Ath MÔCG
SYMMETRY FESTIVAL 2006
BUDAPEST HUNGARY
“GOLDEN ROOT SYMMETRIES OF GEOMETRIC FORMS”
I was born in the city of Aegaleo, Athens, in 1945 and grew up in the port of Piraeus.
My basic, high school education in Greece [Lyceum of Plato], was mainly in Classics including Arts and languages, and my University [London and Athens] studies in Engineering, included a big content of Mathematics.
By my continuous contact, with Engineering and Scientific knowledge, in subjects concerning motion, forces, energy, power etc., I noticed, that, there exist seven (7) basic forms, which appear to derive one from the other and thus related. These forms (relationships) necessary for the creation of a (powerful) work element, from its conceptual idea to materialization are Line, surface, volume per unit time* (mass rate*of unity water density), momentum, force, work (or energy) and power. They are fractions with numerators powers of space (length) and denominators powers of time
L^1![]() /T^0
/T^0![]() ,
L^2
,
L^2![]() /T^0
, L^3
/T^0
, L^3![]() /T^1
/T^1![]() ,
L^4
,
L^4![]() /T^1,
L^4
/T^1,
L^4![]() /T^2,
L^5
/T^2,
L^5![]() /T^2,
L^5
/T^2,
L^5![]() /T^3.
/T^3.
Length (L^1![]() )
and surface (L^2) are timeless (T^0
)
and surface (L^2) are timeless (T^0![]() =1),
Encephalic Concepts.
=1),
Encephalic Concepts.
I will refer here to contents
of various sources which are related to the Greek Culture, Art, and, and
Geometry. In Encyclopaedia Britannica (Vol. 10, 1972, page 829, Greek
Architecture) it is stated:
“To the Greeks fell the role of inventing the grammar of conventional forms on
which all subsequent European Architecture was based. Greek was the patient
genius, with which perfected every element, rarely deviating from the forward
path to invent new forms or new solutions of old problem. This conservative
adherence to older types led to such masterpieces as the Parthenon and
Erechtheum.
According to THEOPHANIS MANIAS [3, 4], the Greek Beauty and the Greek Spirit found in many works of Antiquity, were not ruined by time, death of people or peoples', fanatism and mania. Cities and Sacred Temples were founded according to plans and scientific computations. Religion of the Ancients was the Absolute Beauty, and the Greeks believed as God this Absolute Beauty. Aesthetic Beauty, Optical Beauty, in forms and colours, and Acoustic Beauty in music, Ethic Beauty, found in virtue, and Spiritual Beauty in good learning and knowledge Man sensed, and conquered, all kinds of Beauty, through Love, because Love is the Synectic Substance of the Harmonic Universe. The Ancients had studied this subject, with religious piety. They had observed the existence, of another Beauty, in Nature. Beyond this Harmony, which is Visible, and used, today, by architects, decorators, and generally all those occupied with Aesthetics and Arts, there is another Invisible Geometric Harmony. Circle, Square, Equilateral Triangle, Regular Hexagon, Cube, Pyramids etc., have a Visible Beauty that man senses by his eyes and he finds it in these geometric forms. Symmetries, analogies and other mathematical relationships, were found in the leaves of trees, the petals of flowers, the trunks and branches of plants, the bodies of animals and most important, the human body, which composed an Invisible Harmony, of forms and colours superior than the Visible Harmony. This Invisible Harmony, we find, in all expressions of the Hellenic Civilization.
EVAGELOS STAMATIS (Hellenic Mathematics No. 4 Sec. Ed. 1979), states that THEOPHANIS MANIAS, discovered that the Ancient Sacred Temples of the Hellenic Antiquity, were founded according to Geometrical Computations and measurements. In the distances, between these Sacred Locations, THEOPHANIS MANIAS, observes, application of, the Golden Section. EVAGELOS STAMATIS, also, states that the German Intellectual MAX STECK, Professor of the University of Munich, in his article, which he published in the Research and Progress Magazine, supports that the Western Civilization, Arts, Crafts and Sciences, derive from the influence of the Greek mathematics. The sources that we get knowledge from, about the Greek Mathematics, are the archaeological researches and the literature of the works of the ancient writers.
MATILA GHYKA [1,2], in his books, presents widely, the Golden Section and Geometry in relation to painting, sculpture, architecture of human faces and bodies, as well as bodies of animals, plants, and shells, in relation to logarithmic spiral.
ROBERT LAWLOR[5],similarly, elaborates on these subjects, and additionally, he states, that, the Egyptians, while building the Pyramid, used the ratio 4/SQR[Phi] , for the value of Pi (ratio of the circumference of a circle by its diameter).
MAX TOTH (Pyramid Prophesies Edition 1988), correspondingly, refers to this ratio, as a useful, approximate form. He also states that, the Mathematicians, from HERODOTUS, have modelled an Orthogonal Triangle, whose small perpendicular, is equal to Unity, the bigger one is equal to SQRT(Phi), and its hypotenuse, is equal to Phi [i.e. GOLDEN NUMBER ]. Also, KEPLER refers to the same, triangle (of MAGIRUS) in a letter to his former professor Michael Mastlin- according to Professor Roger Herz-Fischler [8].
Personally while building a conceptual heliotropic machine [Figure 4], a Solar Tracking contrivance for energy, I found GOLDEN RATIO approximate relationship of the maximum azimuthal angle of the Sun [max. day hours], with respect to 360 Deg., around the 38th Parallel, Athens [21 June Greece S. Rise 05:03 –S. Set 19:51, Dif. =14H: 48First = 14.8H, ratio 24H/14.8H=1.62..].
With all above, in mind I was motivated to search further the subject related to the PYTHAGOREAN THEORY, and particularly the PLATONIC TIMAEUS, which gave me the chance to approach THE GOLDEN RATIO, SECTION or NUMBER and its SQUARE ROOT.
In section 53, of PLATO'S "TIMAEUS", PLATO speaks about the shapes of the Four SOLIDS, of their kinds and their combinations. These are Fire (Tetrahedron) Earth (Cube), Water (Icosahedron), and Air (Octahedron). They are bodies and have depth.
The depth necessarily, contains the flat surface and the perpendicular to this surface is a side of a triangle and all the triangles are generated by two kinds of orthogonal triangles the "ISOSCELES" Orthogonal and the "SCALÅÍÅ". From the two kinds of triangles the "Isosceles" Orthogonal has one nature. (i.e. one rectangular angle and two acute angles of 45 degrees), whereas the "scalene" has infinite (i.e. it has one rectangular angle and two acute angles of variable values having, these two acute angles, the sum of 90 degrees).
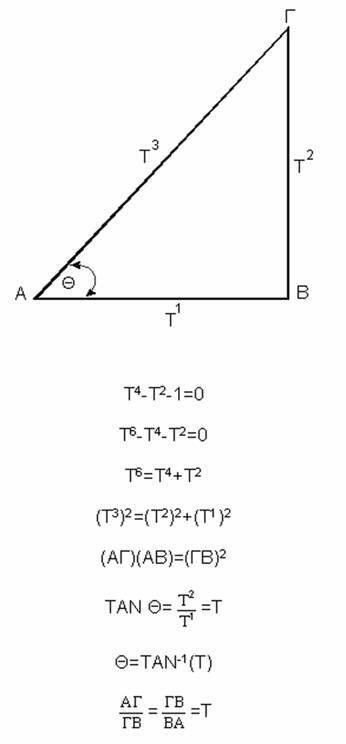
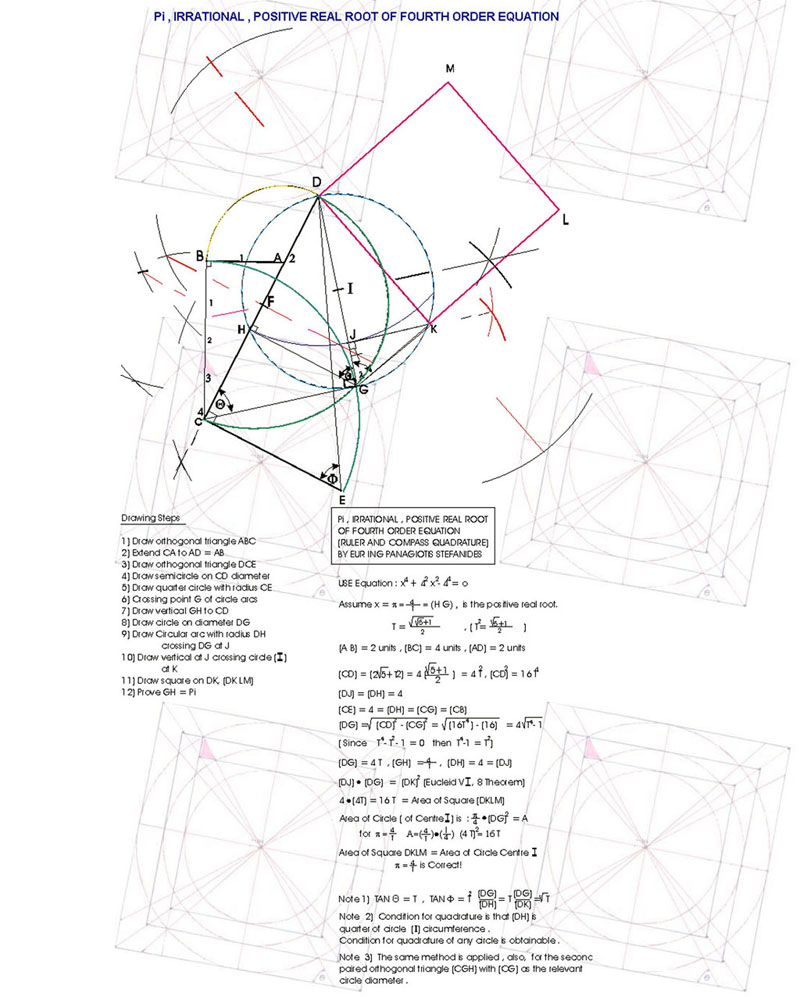
From these infinite natures we choose one triangle "THE MOST BEAUTIFUL". Thus, from the many triangles, we accept one of them as "THE MOST BEAUTIFUL", and we leave those by which the equilateral triangle is constructed (i.e. by using six "scalene" orthogonal triangles, having 30 and 60 degrees their acute angles). The "SCALENE" orthogonal triangle, has its hypotenuse [Stefanides Interpretation] equal to the "CUBE" [T^3], of the value of its horizontal smaller side [T^1] and its vertical bigger side the value of the "SQUARE" [T^2] of its smaller horizontal side.
Thus, by Pythagoras [T^3]^2 =[T^2]^2 + [T^1]^2 or T^6=T^4+T^2 or
T^4 - T^2 - 1 = 0 [ Figure 1 and Figure 2].#
The value of the smaller horizontal side (T) is equal to the Square Root of the GOLDEN RATIO, the ratio of the consecutive sides is equal, again, to the Square Root of the GOLDEN RATIO (geometrical ratio) and the Tangent of the angle between the hypotenuse and the smaller horizontal side is also equal to the SQUARE ROOT of the GOLDEN RATIO (È=51Deg. 49 first 38 sec. 15third ….). The product of the smaller horizontal side and that of the hypotenuse is equal to the "SQUARE" of the bigger vertical side, of this triangle, and at the same time the "PYTHAGOREAN THEOREM" is valid. The values of the sides of this triangle are given by surd numbers, (solution of a fourth degree equation). Reorganizing this triangle, we get another one with the same angle values, which has its bigger vertical side equal to FOUR (4), its smaller horizontal side equal to FOUR divided by the SQUARE ROOT of the GOLDEN RATIO, and its hypotenuse equal to FOUR multiplied by the SQUARE ROOT of the GOLDEN RATIO [the complement of the angle Èis (90- È) =38 Deg. 10 first 21 sec. 44 third….].
Further relating PLATOS, TIMAEUS (section 54) where Plato refers to the "MOST BEAUTIFUL TRIANGLE" and that of the SOMATOIDES (section 31 and 32- stating that “whatever is Born must be Visible Tangible and BODILY”) where the Four Elements are BOUND TOGETHER to become UNITY by the MOST BEAUTIFUL-STEREOID-BOND (which most perfectly unites into one both itself and the things which it binds together, and to effect this in the Most BEAUTIFUL manner is the natural property of PROPORTIONS), analysing these ratios:
FIRE : AIR = AIR : WATER and AIR : WATER = WATER : EARTH and thus FIRE : AIR = AIR: WATER = WATER: EARTH and CONFIGURING them [Stefanides] as TWO PAIRS OF ORTHOGONAL SCALENE TRIANGULAR SURFACES [one pair of orthogonal triangles each with sides T^3 , T^2 , T^1 and the other pair with sides T^2, T^1 and 1 , i.e. four triangular surfaces] BOUND together IN SPACE on a system of three Orthogonal Cartesian Axes of reference (X,Y,Z,), we construct a SOLID [ Figure 3 ], the SOMATOIDES [STEREOID BOND], with coordinates:
(0,0,0),(0,0,T^2), (T,0,0) ,(0,1/T, 1/T^2 ).
This SOLID, with its COMPLEMENT [which is a SOLID too], have a Skeleton Structure of TWO PERPENDICULAR, to each other, ORTHOGONAL TRIANGLES ,the ISOSCELES ,and the MOST BEAUTIFUL, and constitute together 1/8 th of the Great Pyramid Model.[G.P. Model]. The SOMATOIDES to its COMPLEMENT is by VOLUME in GOLDEN RATIO as their sum is to the SOMATOIDES [a third Wedge Shaped SOLID complements the first two, to form ¼ G.P.Model].
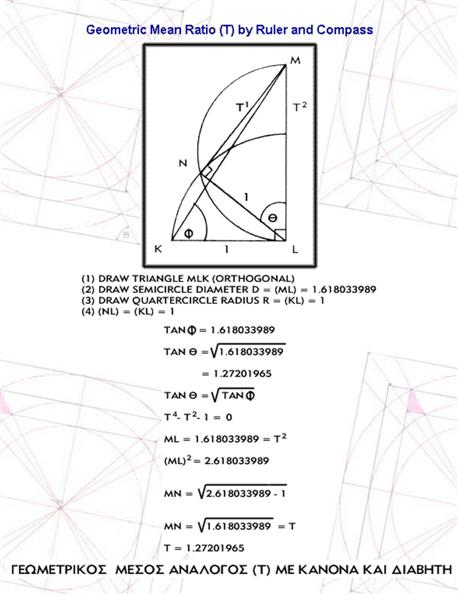
On the basis of the fourth order equation ,above , the COMPASS and RULER GOLDEN ROOT is drawn here, assuming the knowledge of drawing, as such, the GOLDEN SECTION [Phi]=[T^2] [ Figure 5 ]. .http://www.stefanides.gr/gmr.htm
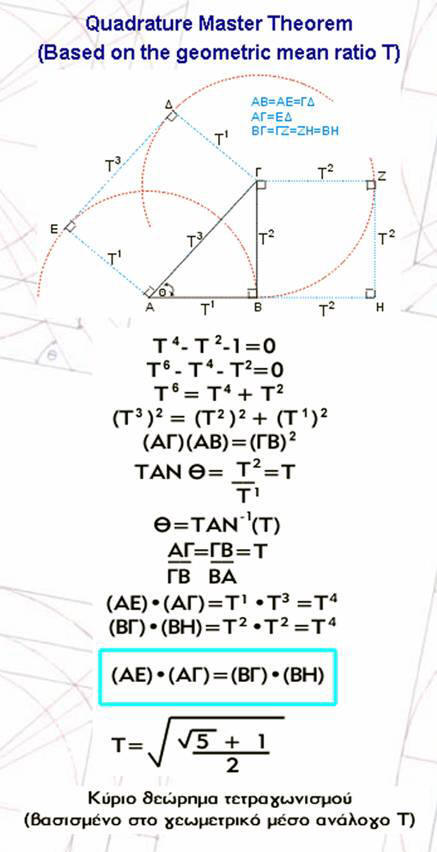
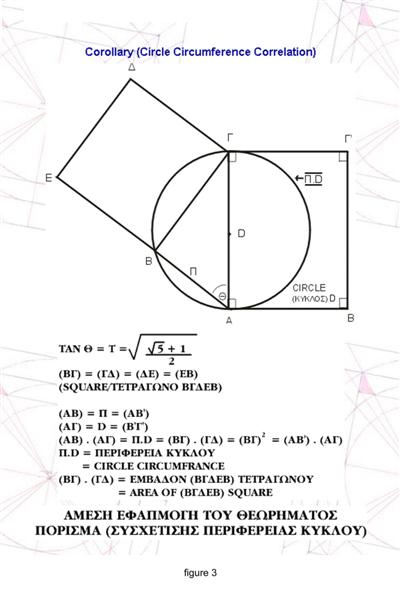
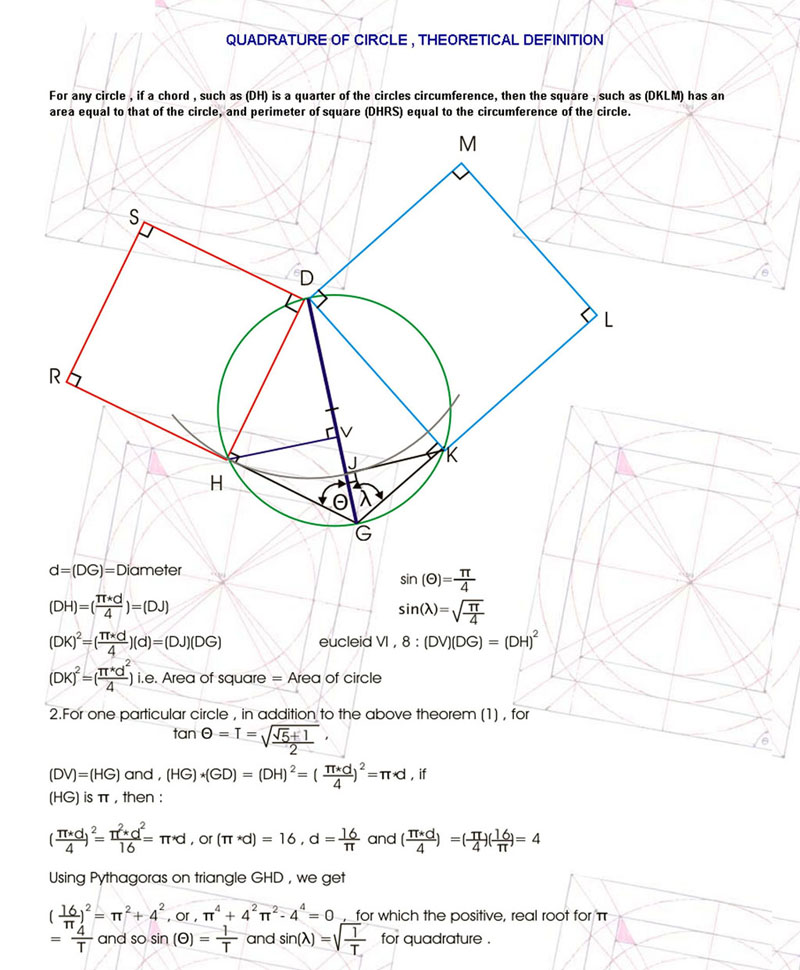
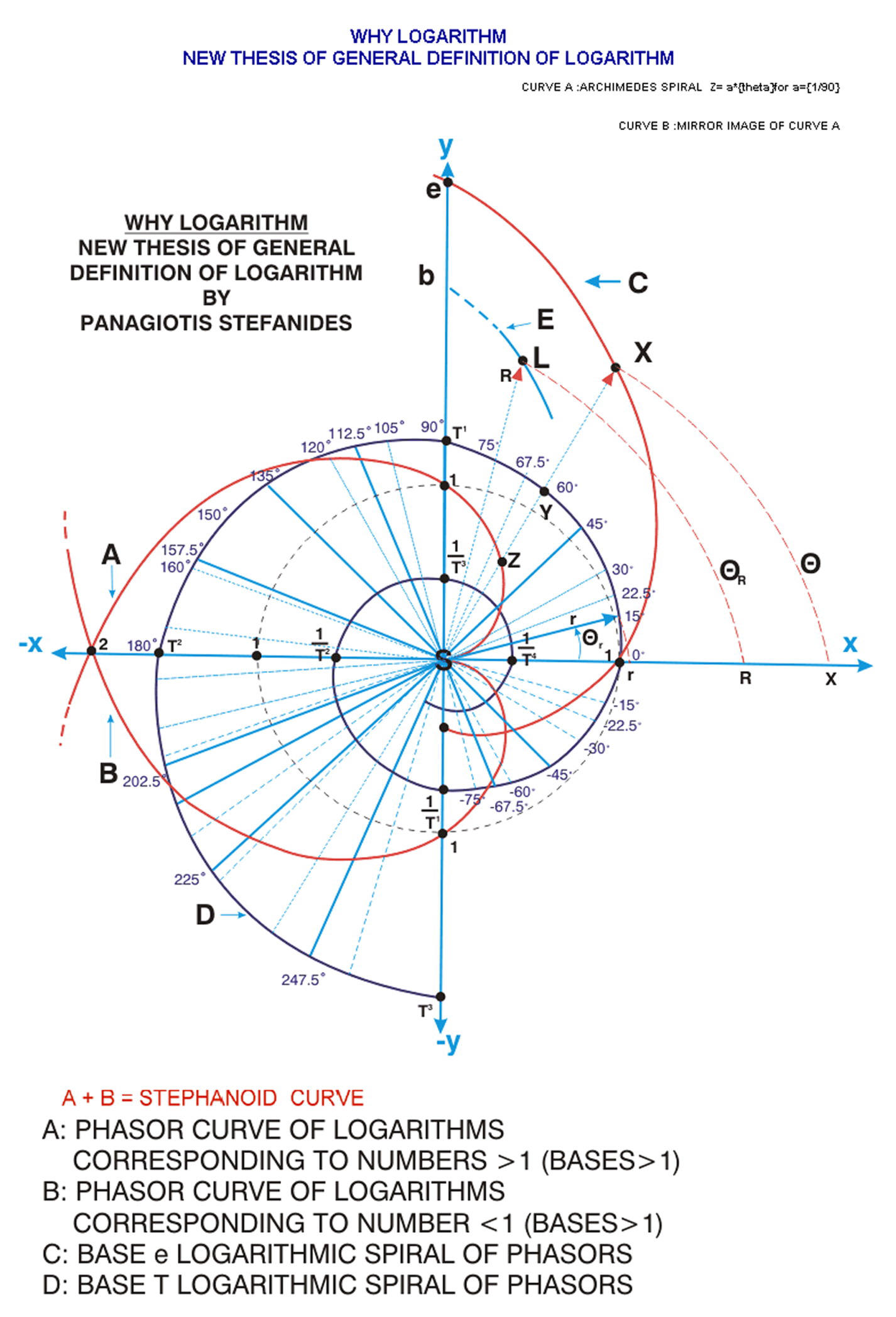
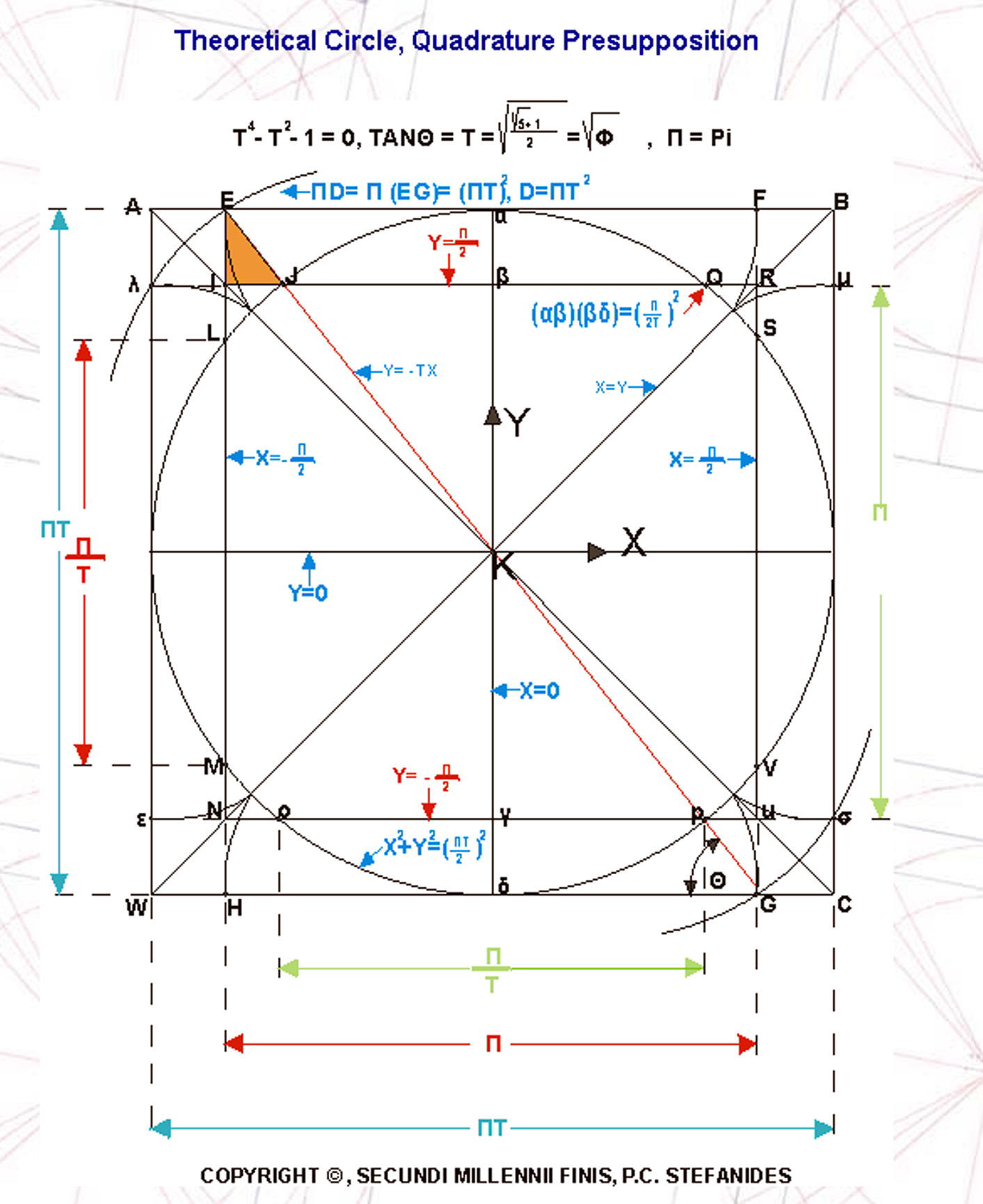
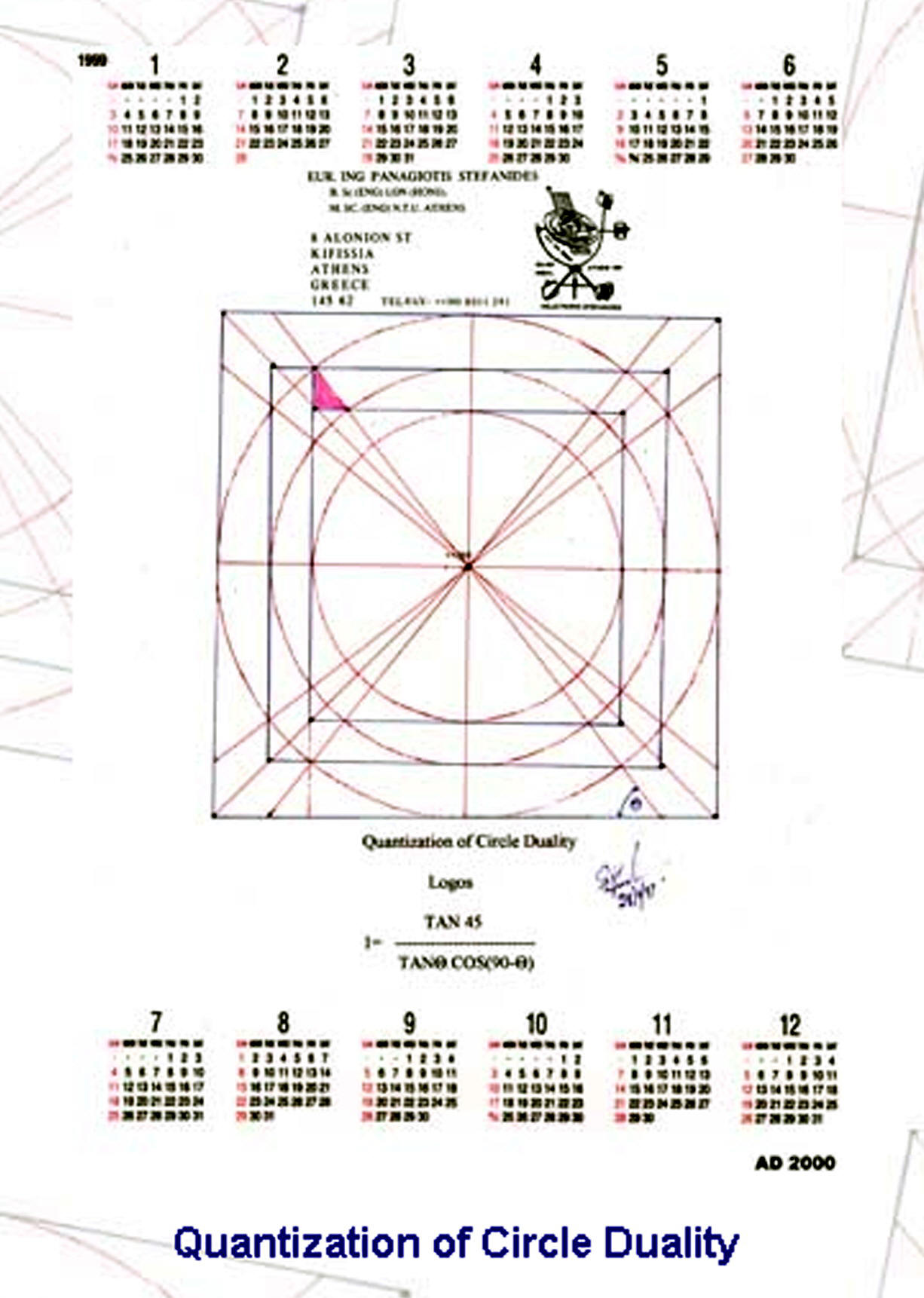
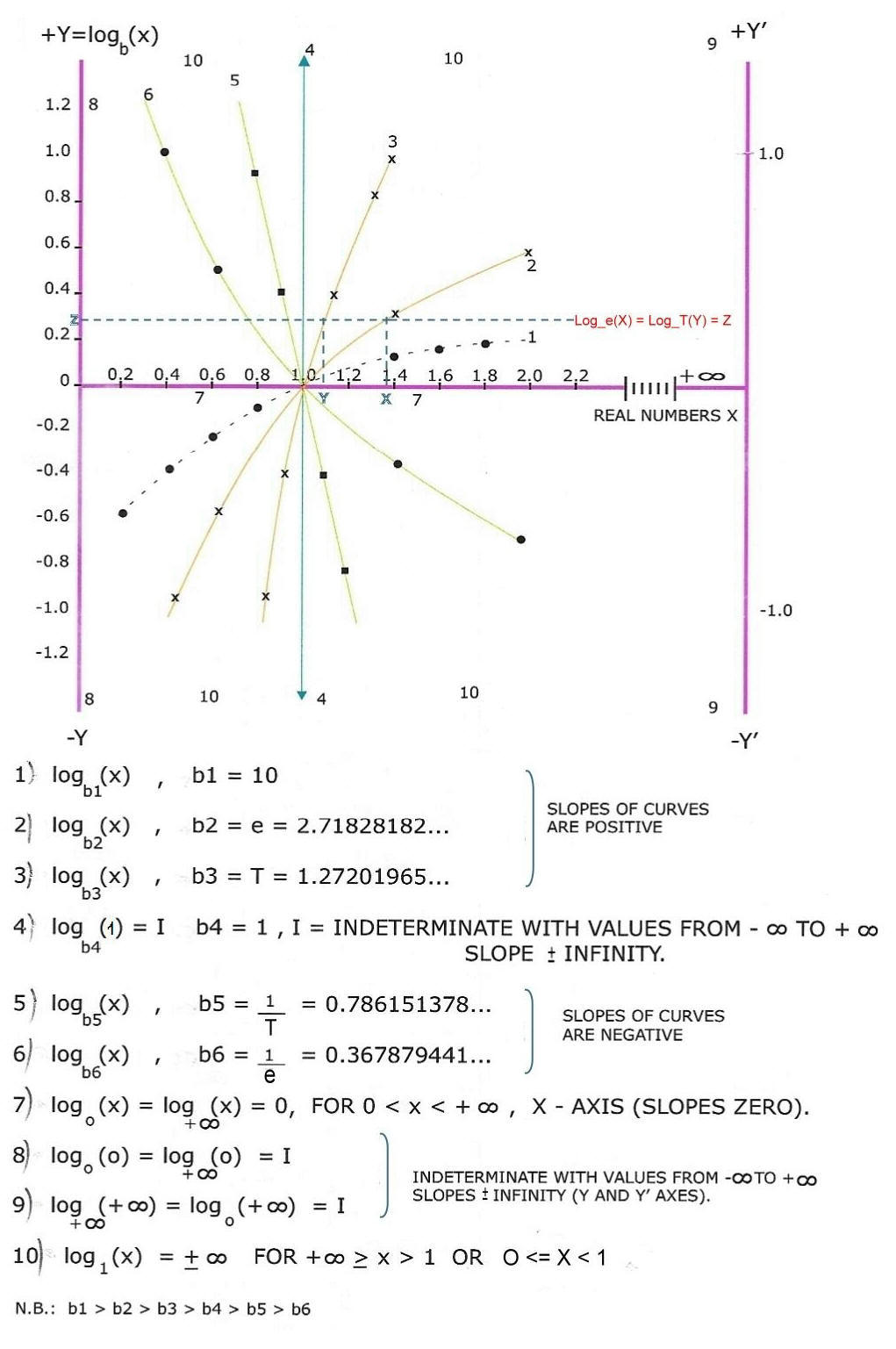
Relating this triangle with circles squares and parallelograms we get Geometric relationships [Figure 6 and Figure 7 ] http://www.stefanides.gr/quadrature.htm http://www.stefanides.gr/corollary.htm and Figure 8 and Figure 9 http://www.stefanides.gr/piquad.htm , http://www.stefanides.gr/quadcirc.htm] involving quadratures and relationships with logarithms and spirals [ Figure 10, Figure 11, Figure 12, Figure 13 and Figure 18] http://www.stefanides.gr/nautilus.htm http://www.stefanides.gr/why_logarithm.htm
[The curve points of the spirals may be obtained graphically by compass and ruler, since expressions of series containing powers may be obtained graphically, step by step, making use of the orthogonal triangle property of multiplying all of its sides by the same length].
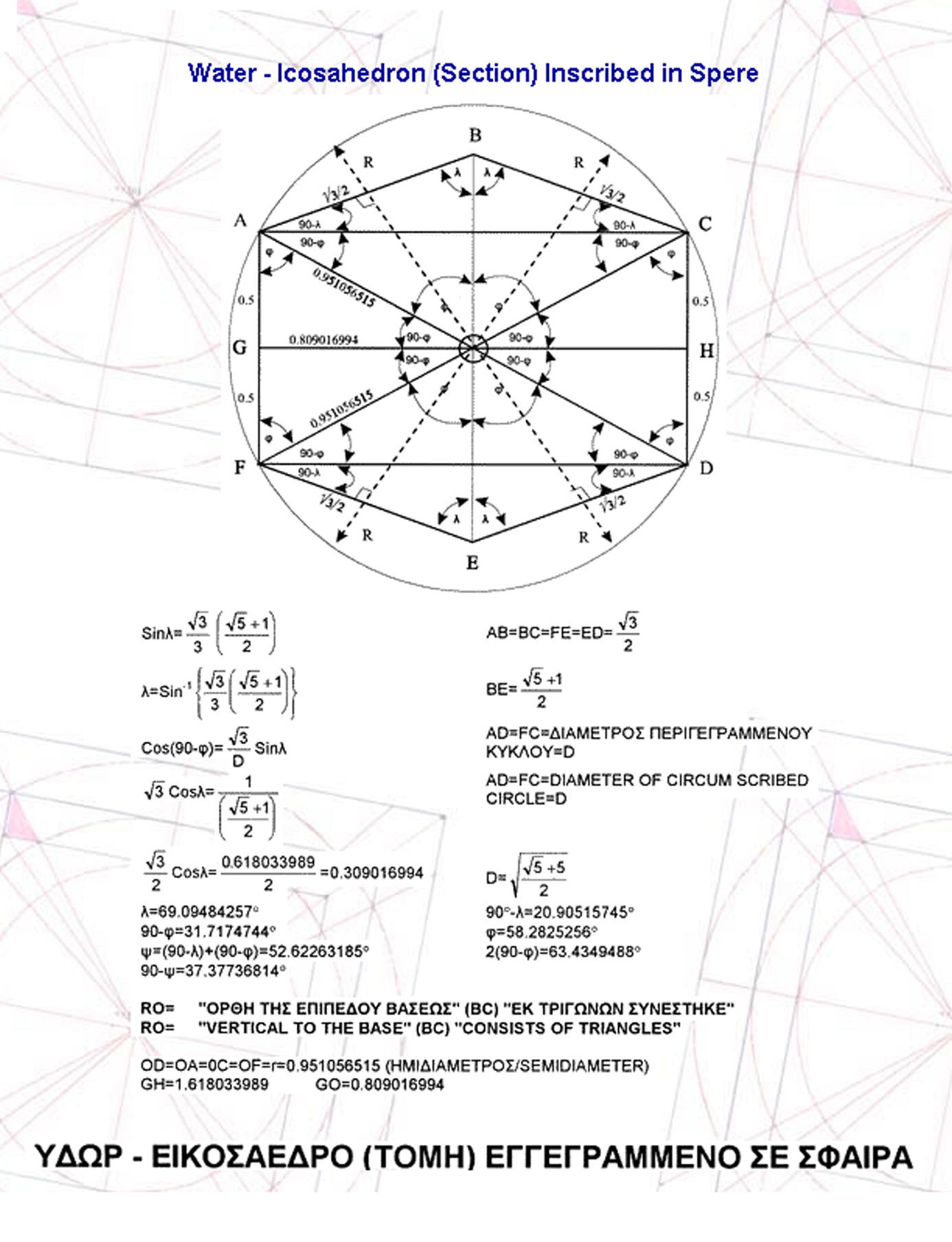
By using sections of the four solids, we find the relationships, between them i.e. the Icosahedron with the Octahedron, the Tetrahedron and the Cube. In addition, if we add selective sections (one next to the other), of the three solids, Icosahedron, Octahedron and Tetrahedron, we find an angle [epsilon 41.8103149.Deg.=2*arctan{1/T^4}=arctan{1/sqrt (1.25)}] which we find also in a section of the Dodecahedron.
So, in this manner we obtain a relationship, of the Dodecahedron with the other Four Platonic Solids. Dodecahedron was considered as the Fifth Solid, mentioned by PLATO in his Timaeus, which “God used it up to Ornament the World”, and was given the name AETHER, by the philosophers.
THE GOLDEN RATIO is found in Section of the Dodecahedron, as also it is found in Section of the Icosahedron, Figure 14, is the section of Icosahedron http://www.stefanides.gr/icosohadron.htm, and Figure 15 Decorated Platonic Solid http://www.stefanides.gr/dec_plastic.htm Figure 16 and Figure 17 Quadrature Presuppositions
http://www.stefanides.gr/theo_circle.htm, http://www.stefanides.gr/quad.htm .
CONCLUSION
Via the GOLDEN ROOTwe get relationships of Geometric structures, Logarithms and Spirals.
It is concluded that by "THE MOST BEAUTIFUL TRIANGLE", PLATO correlates the Elements (UNIFIED THEORY) through the general analogies of their sides i.e. Fire/Air is equal to Air/Water is equal to Water/Earth, is equal to T the GOLDEN ROOT.
Finally, we see that by the use of the METRON or SYMMETRY of the GOLDEN ROOT, we realize PLATO’S statement that all triangles derive from two ORTHOGONAL TRIANGLES the ISOSCELES and the SCALENE.
REFERENCES
1. THE GEOMETRY OF ART AND
LIFE MATILA GHYKA
DOVER PUBLICATION, INC. NEW YORK 1977.
2. LE NOMBRE D' OR
MATILA C. GHYKA
GALLIMARD 1959.
3. PARTHENON
THEOPHANIS MANIAS
PYRINOS COSMOS 1987.
4. TA AGNOSTA MEGALOURGIMATA TON ARCHAEON ELLINON THEOPHANIS MANIAS PYRINOS COSMOS 1981
5. SACRED GEOMETRY ROBERT LAWLOR THAMES AND HUDSON 1982.
6. THE MOST BEAUTIFUL
TRIANGLE - PLATO'S TIMAEUS
P.C.STEFANIDES
FIRST CONFERENCE OF HISTROY AND PHILOSOPHY OF
ANCIENT GREEK MATHEMATICS
MATHEMATICAL SOCIETY RESEARCH INSTITUTE 2, 3 AND 4 MARCH 1989.
7. GEOMETRIC CONCEPTS IN PLATO–RELATED TO ART P.C. STEFANIDES, DEMOKRITEIO UNIVERSITY, 22-23 and 24 Nov. 1991 CONFERENCE OF THE CHAMBER OF ECASTIC ARTS OF GREECE- XANTHE.
8. ROGER HERZ-FISCHLER- Division in EXTREME and MEAN RATIO
WEB LINK REFERENCES
http://curvebank.calstatela.edu/log/log.htm , http://www.direito.up.pt/IJI/taxonomy/term/4 [VOLII/III] http://www.stefanides.gr
ABSTRACT
Under “GOLDEN ROOT SYMMETRIES OF GEOMETRIC FORMS”, my Work and Artwork involving Symmetries of Geometric Forms such as Circles,
Squares, Triangles, Areas, Solids, Spirals and Logarithms, having affinity with the GOLDEN ROOT, which unifies them, shall be presented to the “SYMMETRY FESTIVAL” by exposition of POSTERS and TALK, appreciating that “SYMMETRIES EXPRESS UNIVERSAL LAWS”.
The theory behind this work is based on my, proposed interpretation of Plato’s Timaeus triangles of the structure of matter, “THE MOST BEAUTIFUL” and “THE ISOSCELES” [Pl. Ti 54 B] and also “THE “SOMATOIDES” and “THE STEREOID-MOST BEAUTIFUL BOND” [Pl.Ti.31B, C/32 B] It is additionally based on my special theory, proposed, relating Spirals and Logarithms to various bases.
Of particular interest, to me, is the Form of Nautilus, the kind of which, after measurements of a Shell, found to comply with the logarithm having as base that of the GOLDEN ROOT. By GOLDEN ROOT it is implied the SQUARE ROOT OF THE GOLDEN RATIO.
The Classical Greek word for symmetry, “SYMMETRIA”, means “WITH
MEASURE”, ”IN MEASURE WITH,” “DUE PROPORTION”, “COMMON MEASURE”, “HARMONY”. The concept of “SYMMETRY” contrasts the conditions prevailed before the World was Created, while all elements [FIRE, AIR, EARTH and WATER] were “WITHOUT PROPORTION”[alogos] and “WITHOUT MEASURE”[ametros], and only “TRACES” of them existed ,as all things ,naturally exist in God’s absence. God ,under these conditions, transformed them via “IDEAS” and “NUMBERS”, for them to become “MOST BEAUTIFUL” and “BEST” as possible, contrary to their previous state [Pl. Ti .53B].

Eur Ing PANAGIOTIS STEFANIDES CEng
· Member of the Technical Chamber of Greece [MÔCG], of the Institution of Engineering and Technology [MIET] ,
· Chartered Electrical Engineer [CEng] of the Engineering Council (UK) ,
· Certified Lead Auditor Professional Engineer of the Research Technology and Engineering Division of Hellenic Aerospace Industry S.A. [HAI] ,with experience in
Ø the Fields of Aircraft Engines’ Maintenance Tests,
Ø Manufacturing Co-production programme with SNECMA,
Ø Quality Assurance and Reliability, Company Quality System Audits,
Ø Research and Development of Electronic Systems, Environmental Tests and Certification,
Ø Electromagnetic Compatibility Control and Certification [Notified Body EMC Hellas s.a. ,Affiliate of HAI]
APPENDIX A

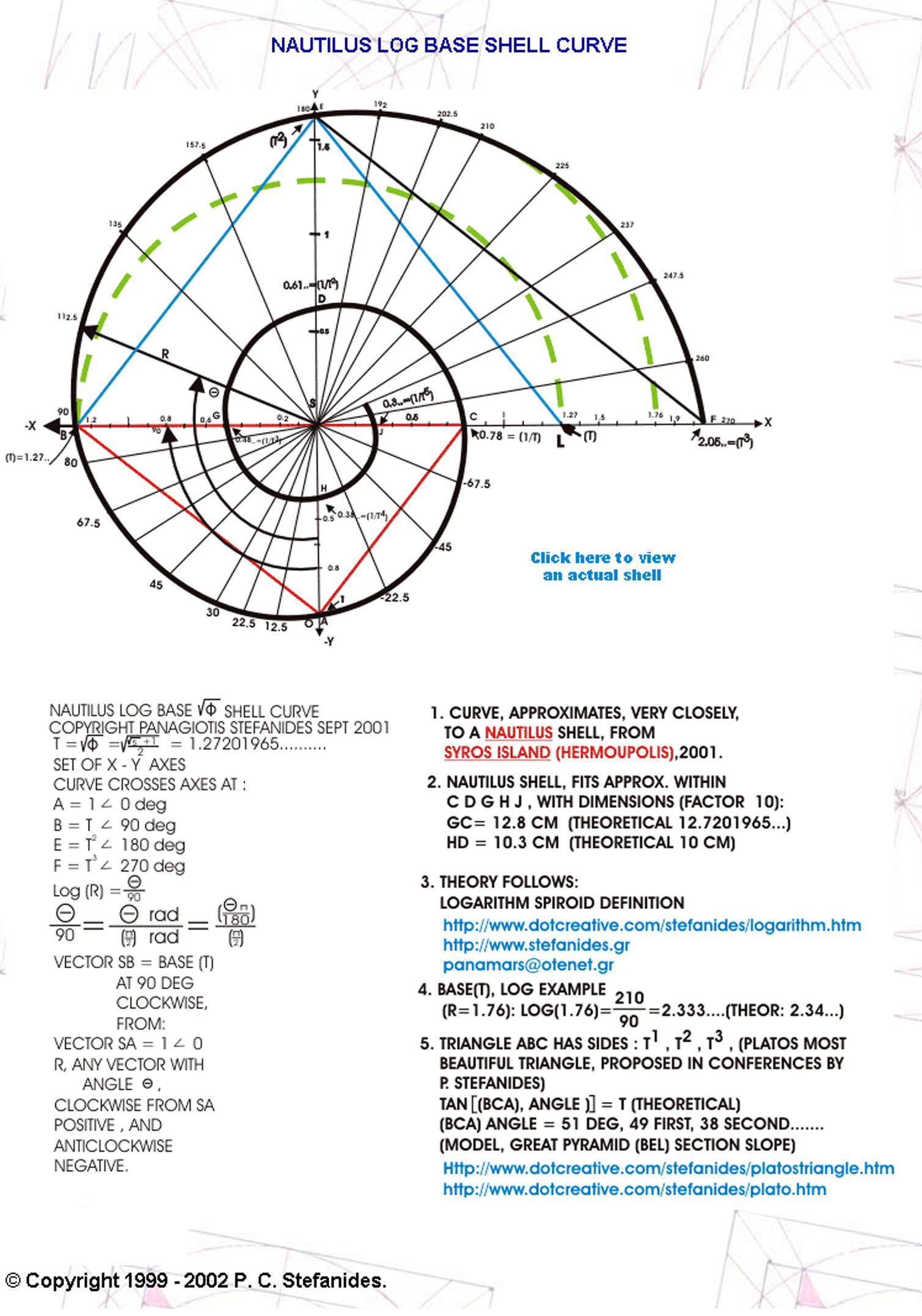

Nautilus Shell


Copyright © 2005 - 2006 Panagiotis. Stefanides. Bibliotheca Alexandrina